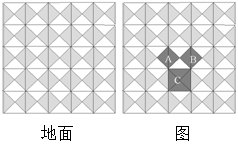
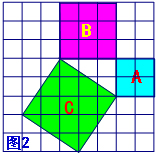
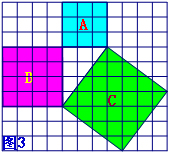
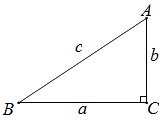
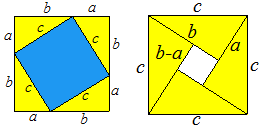
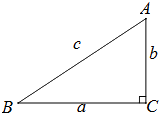
勾股定理
2022-10-12 15:37:00 来源: 撰稿:杨帆 摄影摄像: ; 评论:0 点击:
教学设计

|
|||||
课前微课
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
相关热词搜索:勾股定理
上一篇:“一元一次不等式 (组 )”应用题复习课
下一篇:浅析数学文化在高中教学中的
分享到:
 收藏
收藏